|
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
Régions du Québec |  |
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
 |
Rubriques |  |
 |
 |
|
 |
 |
|
 |
|
 |
 |
 |
Le système bancaire à réserve fractionnelle: la privatisation de l'argent (partie II)
Ceci est la deuxième partie d'une série d'au moins trois articles. La première partie est ici. Cette partie est plus technique (et peut être sautée sans perdre trop de l'aspect qualitatif de la chose) mais n'est pas vraiment plus difficile, il suffit d'un peu plus de patience. Dans cet article, on reprend, généralise et étend l'exemple de la partie I aux transactions bancaires les plus communes. Dans le prochain article (partie III) on parlera de l'inflation dans un système bancaire à réserve fractionnelle et d'un peu d'histoire.
Second exemple: plus technique et plus mathématique mais quand même relativement facile
Maintenant prenons notre banque préférée, la banque Grôssbanque. En décembre 1949 la banque Grôssbanque a imprimé un gros billet de R$ (un gros chiffre) et l'a ensuite converti en beaucoup de billets de 100$ et en argent électronique (des «blips» dans l'ordinateur de la banque centrale au nom de Grôssbanque, librement convertibles en argent papier) auprès de la banque centrale tout à fait légalement. Grôssbanque a donc R$ qui lui appartient, mais elle a aussi, grâce aux dépôts de ses dépositeurs (c'est-à-dire les gens qui ont un compte en banque chez Grôssbanque), D$ dans ses coffres forts. Grôssbanque a donc une réserve d'argent de (R+D)$ (cases jaunes dans le Tableau I). Grôssbanque veut faire de l'argent, elle veut donc prêter un maximum d'argent pour un gagner un maximum d'intérêt dessus. Combien d'argent Grôssbanque peut-elle prêter au maximum? Naïvement on croirait que ce serait R$, l'argent qui lui appartient, ou en tout cas, certainement rien de plus que (R+D)$ l'argent qu'elle entrepose dans ses coffres forts. Éh bien non. Grôssbanque peut prêter beaucoup plus que ce qui lui appartient ou que ce qui est déposé dans ses coffres: Grôssbanque peu prêter tant que les réserves de ses coffres forts représentent plus de T% de ses obligations envers ses clients. Autrement dit, si M$ est le montant maximal que peut prêter Grôssbanque, alors on a que:
T = (R+D)/(M+D) * 100
car l'argent que Grôssbanque doit rendre disponible à ses clients est le M$ qu'elle leurs prête et les D$ qu'ils ont déposé eux-mêmes dans leur compte chez Grôssbanque et l'argent qui est en fait disponible à Grôssbanque est le R$ qui lui appartient et les D$ que ses clients lui ont «prêté». La loi requiert alors que le ratio de ces deux quantités soit d'au moins T%. On peu réécrire l'équation d'en haut comme suit:
M = (100/T)*R + (100/T-1)*D
Donc si T est inférieur à 50 (ce qui est le cas pour la majorité des pays), on aura bien que M, le montant d'argent maximal que peux prêter la banque est supérieur à R+D, l'argent qu'a la banque dans ses coffres! Par exemple, pour T = 10% comme aux États-Unis on a M = 10*R + 9*D! La banque crée donc de l'argent qui n'existait pas avant! Notons par ailleurs que plus T est petit, plus la banque peut créer de l'argent. Si T = 0 (un taux minimal de réserve de 0%) cela veut dire que la banque peut créer et prêter autant d'argent qu'elle le veut, indépendamment de l'argent qu'elle possède vraiment ou de l'argent déposé chez elle par des dépositeurs, c'est la situation au Canada depuis 1994.
Pour ce qui suit, nous utiliserons des mini-simili-tableaux-comptables où sont comptabilisées chaque transactions. Notons que le mot passif indique une dette donc, dans la colonne «peuple passif» on inscrit tout ce que le peuple a de dette. Le mot actif indique un avoir, une possession. Et donc l'avoir net du peuple (la case rouge) est le total de la colonne actif moins le total de la colonne passif. Pour Grôssbanque, on a la même chose, ce qu'elle possède est dans la colonne actif et ce qu'elle doit est la colonne passif. Notons ici que pour ce qui est des cases jaunes, l'argent que tient Grôssbanque, la case jaune foncée (brunâtre/kaki) contient l'argent qu'elle est obligé de tenir «dans ses coffres» afin de maintenir son taux de réserve minimal et la case jaune pâle consiste en l'argent «excessif».
Dans ce qui suit, nous allons chercher à calculer l'argent total qui existe au pays. Comment fait-on cela? Premièrement on doit prendre note que l'argent disponible dans le système, c'est le total de l'argent qui peut être utilisé pour acheter des choses. Mais avec quoi peut-on acheter des choses? On peut acheter des choses avec de l'argent comptant détenu par le particuliers, donc le montant dans la case rose fait parti de l'argent total, on peut acheter des choses avec l'argent dans son compte en banque, donc la case bleue fait parti de l'argent total du système, les réserves minimales de la banque ne peuvent pas être utilisées pour acheter des choses car elles doivent rester dans les «coffres de la banque», donc la case jaune foncée ne contribue pas à l'argent total du système, la case jaune pâle par contre est «l'excédant de réserves» de la banque, elle peut donc en disposer comme elle l'entend, donc la case jaune pâle contribue à l'argent total du système. Notons que toutes les cases dans les colonnes «passif» sont des dettes, donc on ne peut pas acheter des choses avec ça, elles ne contribuent donc pas à l'argent total du système. Notons aussi que même si elles sont des dettes, ces cases jaunes n'enlèvent pas d'argent du système (sauf au moment où elles sont repayées). En effet, si Marie Tremblay a une hypothèque restante de 30000$ et a aussi 30000$ dans son compte en banque, elle peut quand même acheter une voiture de l'année à 30000$, elle n'a donc pas zéro dollars mais bien 30000$ et une dette de 30000$. Par contre, comme un le verra plus tard, si à la place d'acheter sa voiture de l'année et de donner ses 30000$ à quelqu'un d'autre, Marie repaie son hypothèque, alors pouf, ces 30000$ disparaissent en fumée, 30000$ viennent d’être détruits. Mais revenons à nos moutons, on a donc que l’argent total dans le système, le montant qui peux être utiliser pour acheter des chose est la somme des cases rose, bleu et jaune pâle.
Récapitulons: au tout début Grôssbanque a R$ qui lui appartient et "le peuple" a D$ qui lui appartient en argent comptant.
On a donc la situation du Tableau 1:
Tableau 1:

Dans le tableau 1 on met que l'argent créé par Grôssbanque et la Banque centrale sont zéro, ce n’est pas exactement vrai, mais bon, pour simplifier les choses on fait comme si ce l'était, comme si on commençait à zéro. On fait comme si l’argent qui existe au tout début n’a été créé par personne. L’argent qui peut être utilisé pour acheter des choses est l’argent que le peuple a en comptant et l’argent que Grôssbanque a dans ses coffres. Car vu que Grôssbanque n’a aucune obligation de fournir de l’argent à quiconque, toute son argent est libre est Grôssbanque n’a pas besoin de garder des réserves car (T/100)* 0 = 0. On a donc zéro dans la case jaune foncée et le restant R dans la case jaune pâle. Et donc, l’argent total dans le système est D+R comme on aurait pu s’y attendre naïvement.
Après un bout de temps le peuple décide qu’il veut mettre son argent à la banque. Le peuple sort donc son argent de dessous et de dedans ses matelas et ouvre des comptes chez Grôssbanque où la totalité de son argent (D$) est déposé. Donc, dans le Tableau 2, dans la case rose de l’argent comptant du peuple on met zéro car le peuple n’a plus d’argent comptant et dans la case bleu de ses comptes en banque on met D$.
Tableau 2:

Du côté de Grôssbanque, Grôssbanque a une dette de D$ envers le peuple car le peuple lui a prêté D$. Cette dette paie des intérêts faibles (comptes épargnes) ou nuls (comptes chèques), on met donc D$ dans la case verte de la colonne passif de Grôssbanque. La case verte est ce que Grôssbanque doit au peuple car c’est l’argent qui est dans les comptes en banque du peuple. La case verte et la case bleue contiennent et contiendront donc toujours le même montant. Dans les coffres de Grôssbanque il y a maintenant R$ qui lui apparient et D$ déposé par le peuple, donc (R+D)$ en tout. Le montant total d’argent que Grôssbanque doit mettre à la disponibilité du peuple (l’argent du peuple dans ses comptes en banque) est de D$, donc Grôssbanque doit garder T/100% de ce montant en réserve est peut faire ce qu’elle veut avec le reste. On a donc que les réserves minimales qu’elle doit garder sont de (T/100)*D$, on met donc ce chiffre dans la case jaune foncée. Dans la case jaune pâle on met les réserves totales (R+D) de Grôssbanque moins ses réserves minimale, donc : R+D – (T/100)*D. Et donc l’argent total qui peut être utilisé pour acheter des choses est la case bleue plus la case jaune pâle, c’est-à-dire que l’argent total dans le système est de D+R+(1-T/100)*D = (R+(2-T/100)*D)$. Ceci est plus qu’avant ! Il y a (1-T/100)*D$ de plus créé par la banque. Pour donner une idée concrète de ce que cela représente, si le peuple avait un million de dollars (D=1000000) et si le taux de réserve minimal est de 10% (T=10) alors 900000$ (900 miles dollars) serait créés. Il y a donc eu création d’argent (par la banque) car une partie de l’argent du peuple, (1-T/100)*D$, peut être utilisé deux fois en même temps ! Le peuple peut utiliser ses D$ comme il l’entend, mais Grôssbanque peut aussi utiliser (1-T/100)*D$ de ces D$ pour acheter ce qu’elle veut car Grôssbanque n’a besoin de garder que T% des dépôts de ses client(e)s dans ses coffres. Notons que le taux de réserve, l’argent dans les coffres de Grôssbanque (somme des deux cases jaunes) diviser par l’argent qu’elle doit rendre disponible à ses clients (case verte) est (R+D)/D*100% ce qui est plus de T% donc Grôssbanque peut faire plus de prêts au peuple puisqu’elle a des réserves excessives. Notons aussi que vu que par définition, dans la case jaune foncée, on a le montant de la case verte multipliée par T/100, le taux de réserve sera à T% lorsque l’argent libre de Grôssbanque, la case jaune pâle, est à zéro. Tant qu’il reste de l’argent libre à Grôssbanque, Grôssbanque peut prêter plus d’argent au peuple.
C’est bien le cas présentement, comme nous l’avons précédemment calculer au deuxième paragraphe, Grôssbanque peux prêter M$= [(100/T)*R + (100/T-1)*D]$ de plus au peuple (pour des hypothèques par exemple). Pour ce faire, Grôssbanque écrit simplement un crédit de M$ aux comptes du peuple. Les comptes du peuple, la case bleue, ont donc maintenant (D+M)$ comme on peut le voir dans le Tableau 3. Evidemment, la banque ne prête pas cet argent gratuitement, elle prête à un taux d’intérêt relativement élevé. Le peuple contracte donc ainsi une dette à intérêt élevé auprès de Grôssbanque : les deux cases beiges. La case verte est l’argent que Grôssbanque doit fournir au peuple s’il décide de vider ses comptes en banque chez Grôssbanque, on a donc D+M dollars dans cette case.
Tableau 3:

Mais d’où provient donc les M$ = [(100/T)*R + (100/T-1)*D]$ que Grôssbanque prête ainsi au peuple ? Il y a premièrement les R$ que Grôssbanque possède, mais ensuite il y aussi les (M-R)$ = (100/T-1)*(D+R)$ que Grôssbanque crée de toutes pièces mais qui n'existe réellement pas et donc qu'elle doit «détruire» à un moment donné. Notons que ce montant d’argent est bien plus que le montant d’argent qu’y existait au début : si le taux minimum de réserve est de 10% alors T = 10 le montant d’argent créé de toutes pièces par Grôssbanque est 9*(D+R) donc neuf fois le montant total d’argent initial ! Bien entendu comme, pour Grôssbanque, l'argent qu'elle crée de toutes pièce est pour elle comme une sorte d'emprunt sans aucun frais d’intérêt qu'elle peut prêter à des taux d'intérêts élevés, Grôssbanque est peu encline à détruire cet argent créé de toutes pièces.
Mais qu’arrive-t-il si Marie, une personne du peuple, sort x$ (en argent comptant disons, car si elle donne un chèque ou paie débit rien ne se passe de notre point de vu) pour acheter une maison ? Premièrement si Marie sort x$ comptant, alors elle a x$ en argent comptant (ou «libre») et doit soustraire x$ au montant de son compte en banque (case bleue). Deuxièmement les réserves de Grôssbanque sont aussi diminuées de x$ car Grôssbanque doit puiser dans ses réserves pour donner x$ à Marie, donc Grôssbanque a donc des réserves de (R+D-x)$ . Mais de par la loi Grôssbanque doit maintenir des réserves d’au moins (T/100)*(D+M-x)$ = [D+R-(T/100)x]$. Grôssbanque se retrouve donc dans une situation illégale, ses réserves sont à court de (1-T/100)*x$, ce que le note en mettent (1-T/100)*x dans la case jaune pâle passif. C'est-à-dire que Grôssbanque est dans le rouge pour ce qui est de son Argent «libre». Par définition on définit y comme étant y = (1-T/100)*x afin de se simplifier un peu la vie. Notez bien aussi que comme le peuple a autant d’argent avant que Marie ait retiré de l’argent qu’après mais que Grôssbanque se retrouve avec un déficit de y$ dans son argent «libre» après le retrait cela veut dire qu’en retirant x$ en argent comptant, Marie a entraîné la destruction de y$. Plus concrètement, si Marie a retiré 100 000$ et que le taux de réserve minimal est de 10% alors y$ = 90 000$ et donc Marie aurait forcé la banque à détruire 90 000$ de l’argent qu’elle avait préalablement créé. Vous noterez que dans le Tableau 4. Grôssbanque a en effet créé y$ de moins que dans le Tableau 3.
Tableau 4:

Grôssbanque a alors deux solutions, soit elle emprunte de l’argent d’une autre banque, soit elle emprunte directement à la banque centrale. Comme on suppose ici que Grôssbanque représente l’ensemble des banque du pays, Grôssbanque emprunte y$ de la banque centrale à un taux d’intérêt moyen (plus haut que le taux d’un compte épargne mais plus bas qu’un taux hypothécaire). Grôssbanque emprunte donc cet argent est la laisse dans ses coffres afin de satisfaire à son taux de réserve minimum requis comme on peut le voir dans le Tableau 5. Mais ces y$ que la banque centrale a prêté à Grôssbanque viennent d’être créé par la banque centrale, soit en les imprimant sur du papier pour ensuite les livrer à Grôssbanque ou plus probablement simplement en l’inscrivant dans le système informatique. On rajoute donc y$ = (1-T/100)*x$ aux réserves de Grôssbanque ce qui a pour effet de remettre la case jaune pâle à zéro. Par contre, Grôssbanque contracte une dette de y$ envers la banque centrale, on l’inscrit dans la case orange à intérêt moyen. Notons que les y$ créé par la banque centrale remplacent exactement les y$ détruit lors du retrait par Marie de x$. L’effet global donc de retirer de l’argent à son compte en banque (dans un système de réserve fractionnelle où T n’est pas zéro) est de détruire de l’argent créé par des banques privées et le remplacer par de l’argent créé par la banque centrale. Contrairement à l’argent qu’elle crée elle-même, une banque privée doit payer des intérêts (quoi que moins que le peuple en général) sur l’argent créé ainsi par la Banque centrale. Donc si plusieurs personnes commencent à retirer de l’argent en même temps d’une banque privée cela peut lui coûter très cher (c’est ce qui se passe actuellement avec la banque anglaise Northern Rock) et même si les gens retire assez d’argent pour qui la banque centrale ne veuille plus lui prêter de l’argent alors la banque privée peut faire faillite.
Tableau 5:

Par la suite Marie donne ses x$ en argent comptant à Julie en échange d’une belle maison en Gaspésie. Il n’y a alors aucun changement dans notre Tableau car il n’y pas de transaction entre Grôssbanque et le peuple, seulement un échange entre une personne du peuple et une autre.
Tableau 6:

Évidemment, Julie ne désire pas garder un gros montant d’argent ayant la valeur d’une maison en argent comptant chez elle, donc elle va porter cet argent à la banque, elle dépose donc x$ dans son compte chez Grôssbanque. Ceci a pour effet qu’elle n’a plus d’argent comptant, donc la case rose est remise à zéro. Cela ajoute aussi x$ aux comptes du peuple donc on ajoute x à la case bleu et à la case verte. Et finalement cela rajoute x$ aux réserves de Grôssbanque qui sont donc maintenant de (D+R+y). Comme les réserves minimal que doit avoir Grôssbanque sont de (D+M)*(T/100)=D+R, Grôssbanque a y$ d’argent libre, comme on peu le constater dans le tableau 7.
Tableau 7:

Comme Grôssbanque a y$ d’argent libre, elle peut faire ce qu’elle veut avec cet argent et, par exemple, elle peut repayer sa dette envers la banque centrale. Grôssbanque repaie donc sa dette envers la banque centrale, pour ce faire elle utilise sont argent «libre» et donc la case jaune pâle est remise à zéro. Puis, comme Grôssbanque a repayé sa dette, la case orange est aussi remise à zéro et l’on obtient le Tableau 8 qui est en fait la même chose que le Tableau 3 car on est revenu à la même situation. Les y$ que Grôssbanque donne à la Banque centrale soit sous forme papier soit sous forme électronique sont alors effectivement «détruits» par la banque centrale. Si l’argent était sous forme électronique alors elle est réellement détruite, si l’argent était sous forme papier alors (si l’argent est toujours en bon état) l’argent est tout simplement retiré de la circulation et placé dans un coffre fort pour être entreposé jusqu’au moment ou la banque centrale aura besoin de créer plus d’argent papier, alors la banque centrale pourra sortir cet argent et le mettre en circulation.
Tableau 8:

Maintenant qu’arrive-t-il si Marie arrive à économiser assez d’argent pour payer une partie ou le tout de son hypothèque ? Marie fait un paiement de H$ à la banque. Comment procède-t-on pour effectuer le paiement ? Premièrement, elle paie H$ de ses dettes donc les cases beige, les dettes du peuple envers Grôssbanque, diminuent de H$. Deuxièmement, elle effectue ce paiement à partir de sont comte bancaire donc H$ est débité de son compte donc on enlève H à la bleu et à la case verte. Mais puisque la case verte a changé, les réserves minimales que doit garder Grôssbanque ne sont plus les mêmes. Les réserves minimales sont maintenant (T/100)*(D+M-H)$ et donc il y a T*H/100$ qui devaient être dans la réserve mais qui sont maintenant «libérés». Et donc globalement, il y a H$ de moins parce que le peuple a perdu H$ en repayant la banque mais la banque a T*H/100$ de plus dont elle peut disposer comme elle veut et donc en somme (1-T/100)*H$ que Grôssbanque avait créé ont été détruits comme vous le constaterai en comparant le Tableau 9. avec le Tableau 8. Et donc si l’hypothèque H de Marie était de 100 000$, et que le taux de réserve minimal est de 10%, en repayant son hypothèque de 100 000$ il y 90 000$ qui sont partis en fumé.
Tableau 9:

Évidemment, Grôssbanque va la reprêter un maximum d’argent à quelqu’un d’autre afin de pouvoir gagner de l’intérêt dessus. Et donc, par exemple, Grôssbanque pourrait prêter H$ (c’est évidemment le maximum qu’elle peut prêter si elle recrée les (1-T/100)*H$ qui viennent de disparaître) à Jean afin qu’il s’achète un voiture de l’année. On retrouve alors exactement la même situation qu’on avait avant que Marie paie son hypothèque comme on peut le constater en comparant les Tableau 10. et 8.
Tableau 10:

Mais notez que si Jean pense que ça va mal au travail et qu’il risque de perdre son emploi ou que son salaire va être coupé ou va stagner alors il ne voudra pas emprunter pour acheter une voiture. Et si Grôssbanque trouve personne pour emprunter plus d’argent alors les (1-T/100)*H$ ne réapparaîtront pas et il y aura réellement moins d’argent dans le système.
C'est pour ça qu'à la télé ou dans les journaux, on parle tant du «sentiment des consommateurs» ou de «l’indice de confiance des consommateurs». Et c'est pour ça qu'on incite subtilement les gens à dépenser et non pas à économiser. Car, dans le système actuel de réserve fractionnelle, même si individuellement chaque individu à avantage à économiser devant une économie ralentissente, si les consommateurs en général sentent que les temps vont être durs et se mettent à économiser et payer leurs dettes au lieu de dépenser et consommer, des sommes massives d'argent vont être détruites (non seulement ça, mais la «vitesse» de l'argent, la vitesse avec l'argent change de mains, diminue, ceci a le même effet que la destruction de l'argent comme nous allons le voir dans la partie III de cette série d'articles). Et qui dit moins d'argent dit une économie qui roule moins vite. Qui dit moins d'argent, dit aussi pas assez d'argent pour acheter tous les biens produits. Les entreprises ont donc le choix entre ne pas vendre leurs produits, ou les vendre en dessous du prix coûtant. Ceci précipitera donc une récession. Cette sorte de récession est ce que les économistes (une bande de crack-potes avec des oeillères plus grosses que la tête) et les médias (soit totalement ignorants, soit décevant intentionnellement les gens) aiment à appeler une «crise de surproduction» (cette expression me fait tellement rire, elle est tellement absurde, elle est pire que le double-speak orwellien et l'absurde d'Ionesco combinés, comment se peut-il que l'on produise trop alors qu'il y toujours pleins de gens dans la pauvreté la plus abjecte, pleins de gens sans nourriture, sans maison, avec que peu de vêtements, alors qu'il y a toujours pleins de gens qui travaille à se briser le dos mais qui arrivent à peine joindre les bouts?!? comment peut-il y avoir surproduction dans de telles circonstances??). La solution dans le système actuel? La destruction des moyens de production: la fermeture d'usines et d'entreprises par la faillite (une partie de leurs équipement et infrastructures se font acheter à rabais par les plus grosses entreprises qui ont assez d'argent en réserve pour survivre la récession (un exemple actuel de ça est l'annonce hier du possible achat de Nothern Rock par HSBC ou Lloyds en Angleterre) mais ne sont pas utilisées dans l'immédiat car les stocks sont suffisant pour satisfaire à la «demande») pour les plus petites qui sont plus vulnérables et la fermeture temporaire des moyens de productions des plus grosses entreprises. Cela «résout» le problème de deux façons: premièrement, la masse d'employé(e)s licencié(e)s ne peuvent plus se permettre «le luxe» d'économiser et de payer leurs dettes (ce qui détruit l'argent), certain(e)s doivent même s'endetter (ce qui crée de l'argent) de nouveau juste pour survivre, deuxièmement, les petites et moyennes entreprises ayant été éliminées il y a moins de produits sur le marché, l'offre et plus faible, il y a donc une sorte de rééquilibrage de l'offre et de la demande, mais plus important encore, les grandes entreprises se trouvent en position de quasi-monopole, elles peuvent donc fixer leurs prix (au dessus du prix coûtant) sans égare au fait que la population en général n'a plus les moyens de payer ces prix (parce qu'il n'y a plus autant d'argent le système), de toute façon, la population peut toujours s'endetter (ce qui crée de l'argent) afin de se loger et de se nourrir. Donc en fait, une récession n'est pas si mal (c'est même très bien), pour les plus grandes entreprises car cela élimine la compétition et leur permet de garder une position dominante, et comme bonus, elles peuvent se rééquiper, augmenter leurs concessions d'exploitations de ressources naturelles (terres agricoles, champs de pétrole, quotas de production, mines, etc.) et agrandir leur infrastructure à peu de frais en achetant les résidus de leurs défuntes compétitrices. Des récessions à intervalles réguliers sont presque essentielles aux grandes entreprises (et banques) afin de préserver leur position dominante, d'ailleurs ces compagnies (mais surtout les banques) ne manquent pas d'inciter régulièrement la banque centrale à provoquer des récessions, et comme les dirigeant(e)s de la banque centrale sont des banquièr(e)s qui ont déjà et qui retournerons sûrement travailler dans le secteur privé les banques privées et les entreprises qu'elles représentes n'ont pas trop de mal à se faire entendre. Mais le plus drôle dans tout ça, c'est qu'on entend souvent dire que le problème de surproduction est inhérent au capitalisme. Strictement parlant c'est totalement faux, ce problème est inhérent au système bancaire que nous utilisons, par exemple, dans un pays où l'on utiliserait un système bancaire de Crédit Social (voir la section «articles de mise en contexte» du blogue) on n'aurait pas de problème inhérent de «surproduction» et ce serait toujours un système capitaliste (dans le sens que les moyens de productions peuvent toujours être de la propriété privée).
Après qu’un an soit passé (ou quelconque période) le temps de verser et de collecter les intérêts est arrivé. Grôssbanque doit payer de faibles (ou pas du tout si c’est un compte chèque) intérêts au peuple sur le montant dans la case verte du Tableau 10. et le peuple doit payer des intérêts élevés sur le montant inscrit à la case beige. Disons que la banque reçoit I$ en intérêts et dois payer i$ en intérêts au peuple. I est un montant supérieur à i sinon la banque ferrait vite faillite et dans la pratique ce nombre est immense. Soit donc P$ = (I-i)$ le montant nette que Grôssbanque reçoit du peuple. Alors le peuple doit payer un montant P$ à Grôssbanque. Comment faire ? La case verte qui est égal à la case bleu est le montant d’argent que Grôssbanque doit au peuple, il suffit donc de soustraire P de ces deux cases. Mais alors, le montant de réserve minimum devient (T/100)*(D+M-P)$= [D+R-(T/100)*P]$ ce qui veut dire que l’argent «libre» de la banque est (T/100)*P. Par contre le peuple a perdu P$ donc globalement il y a eu destruction de (1-T/100)*P$ et la situation est comme illustrée au Tableau 11.
Tableau 11:

Mais évidemment, encore une fois, Grôssbanque voulant maximiser ses profits va prêter autant d’argent qu’elle peut dans la limite du légal. Le montant maximum K$ qu’elle peut prêter est tel que (D+R)/(K+[D+M-P]) = T/100. Ce qui signifie que K = P. Donc Grôssbanque peut (créer et) prêter P$ au peuple. Puisque Grôssbanque prête P$ de plus au peuple, en plus du M$ déjà prêté, on devra ajouter P aux cases beiges. Grôssbanque doit mettre l’argent à disposition du peuple dans leur comptes en banque et donc on doit aussi ajouter P à la case bleu et à la case verte. Pour ce qui de l’argent «libre» de la banque on sait qu’il n’en restera plus car on a choisi de prêter le maximum d’argent. On se retrouve donc avec la situation suivante telle que décrite par le Tableau 12.
Tableau 12:

Et on voit donc qu’au bout du compte, le montant total d’argent est le même qu’avant que les intérêts soient payés sauf que maintenant le peuple est plus endetté et plus pauvre et Grôssbanque est plus riche.
Mais maintenant qu’arrive-t-il si la population du pays augmente et production du pays augmente ? Il y a plus de gens et plus de produit donc on a besoins de plus d’argent dans le système pour pouvoir continuer toutes les transactions quotidiennes au même rythme qu’avant. Comment fait-on pour augmenter le quantité d’argent dans le système ? C’est assez bizarre mais c’est tout de même assez simple. Si la banque centrale décide qu’on doit augmenter la quantité d’argent en circulation, elle crée N$ disons et elle les prête (de façon presque permanente) aux banques privées à un taux d’intérêt moyen. Grôssbanque reçoit donc un prêt de N$ de la banque centrale et donc les réserves de Grôssbanque augmentent de N$ mais aussi ses dettes à intérêt moyen (case orange) augmentent de N$. On se retrouve donc dans la situation du Tableau 13.
Tableau 13:

Évidemment, Grôssbanque ne va pas laisser l’argent se reposer dans ses coffres car elle doit payer de l’intérêt sur cet argent et donc si l’argent reste dans ses coffres à rien faire Grôssbanque va perdre de l’argent. Grôssbanque veut faire comme d’habitude et prêter le plus d’argent possible à un haut taux d’intérêt. La question est donc de savoir combien d’argent Grôssbanque peut prêter au peuple. Les réserves de Grôssbanque sont maintenant (R+D+N)$. Le montant maximal qui K$ qui peut être prêté doit satisfaire à l’équation (R+D+N)/(D+M+K)=T/100 ce qui impose que K = (100/T)*N. Ce qui veut dire par exemple, si T = 10, que Grôssbanque peut prêter 10 fois le montant d’argent qui lui a été prêté par la banque centrale. Ceci veut dire que Grôssbanque crée 9*N$ à partir de rien, totalement gratuitement et ensuite prête cet argent au peuple à des taux d’intérêts élevés. Pour ce qui est du N$ que la banque centrale lui a prêté elle le prête aussi à un taux d’intérêt élevé, plus élevé que le taux moyen auquel la banque centrale lui a prêté. On se retrouve donc dans la situation décrite par le Tableau 14.
Tableau 14:
Ce qui est le plus scandaleux est que, à toute fin pratique, cette méthode de créer l’argent est l’unique méthode utilisée. Ceci veux dire que (si T = 10 mais dans les faits T tourne plus au tours de 2) pour chaque dollars créé par le gouvernement, 9 dollars sont créés par des banques privées. Non seulement ça mais pour créer plus d’argent il faut absolument que quelqu’un quelque part s’endette et donc si un jour toutes les dettes étaient payées il ne resterait presque plus d’argent ! En fait la situation est encore pire que ça parce que pour des pays comme le Canada, l’Angleterre et la Suède, T=0 et donc les banques privées peuvent créer autant d’argent qu’elles le souhaitent. Et pour les autres pays, le taux minimal de réserve ne s’applique pas sur tous les comptes bancaires mais seulement les comptent courants (les comptes chèques) et donc les banque peuvent créer autant d’argent qu’elles le veulent tant que cet argent se retrouve dans des comptent épargne. Les banque doivent seulement satisfaire à la contrainte que R/C >T/100 où R est le montant d’argent que la banque a dans ses coffres, C est la somme des montants de tous les comptes courants de cette banque et T est le taux minimal de réserve.
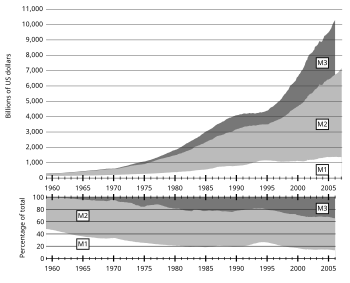
Pour mieux comprendre l’amplitude de l’argent créé par les banques privées regardez le graphique ci-dessous qui se rapporte aux dollars étasuniens. M1 est l’argent «libre» des banques et les comptes courants. M2 est, grosso modo, les M1 plus les comptes épargnes, les comptent d’investissement, etc. et M3 est, grosso modo, M2 plus les dollars étasuniens à l’extérieur du réseau financier étasunien (en Suisse par exemple).
Dans les prochaines parties de la série nous aborderons l’inflation et les cycles économiques.
-matchafa
matchafa.quebecblogue.com
Autres parties de la série: Partie I, Partie II, Partie III, Partie IV
sources:
- http://en.wikipedia.org/wiki/Fractional_reserve_banking
- http://en.wikipedia.org/wiki/Reserve_requirement
- http://en.wikipedia.org/wiki/Local_currency
- http://fr.wikipedia.org/wiki/Banque_du_Canada#Histoire
- http://en.wikipedia.org/wiki/Bank_of_Canada#History
- http://en.wikipedia.org/wiki/Royal_Canadian_Mint
- http://en.wikipedia.org/wiki/Full-reserve_banking#Monetary_reform
- http://fr.wikipedia.org/wiki/Cr%C3%A9dit_social
- http://fr.wikipedia.org/wiki/Finance_islamique
- http://en.wikipedia.org/wiki/Islamic_banking#Principles
- Lois sur la Banque du Canada
- http://en.wikipedia.org/wiki/Money_supply
 |
 |
 |
 |
G20 Special |  |
 |
 |
|
 |
 |
|
 |
We offer many independent reports and testimonies...

List of actions held during this "counter-summit" in Toronto You may also want to visit these alternative media in Toronto: G20 Alternative Media Centre http://2010.mediacoop.ca Media Co-op Toronto http://toronto.mediacoop.ca Toronto Community Mobilization www.attacktheroots.net |
 |
 |
 |
 |
 |
 |
 |
CMAQ: Vie associative |  |
 |
 |
|
 |
 |
|
 |
 Quebec City collective: no longer exist. Get involved ! |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
Ceci est un média alternatif de publication ouverte. Le collectif CMAQ, qui gère la validation des contributions sur le Indymedia-Québec, n'endosse aucunement les propos et ne juge pas de la véracité des informations. Ce sont les commentaires des Internautes, comme vous, qui servent à évaluer la qualité de l'information. Nous avons néanmoins une
Politique éditoriale
, qui essentiellement demande que les contributions portent sur une question d'émancipation et ne proviennent pas de médias commerciaux.
This is an alternative media using open publishing. The CMAQ collective, who validates the posts submitted on the Indymedia-Quebec, does not endorse in any way the opinions and statements and does not judge if the information is correct or true. The quality of the information is evaluated by the comments from Internet surfers, like yourself. We nonetheless have an
Editorial Policy
, which essentially requires that posts be related to questions of emancipation and does not come from a commercial media.